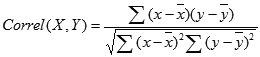BuckChuker
New Member
- Joined
- Apr 30, 2020
- Messages
- 3
- Office Version
- 2010
- Platform
- Windows
Rank (Spearman) Correlation of Non-Adjacent Values in Excel in Single Formula
1. In a single formula, I am trying to get the Rank (Spearman) correlation between two arrays. One of the arrays contains non-adjacent values. I can get the Pearson correlation with this formula:
=CORREL(CHOOSE({1;2;3},U7,AM7,BE7),HR1:HT1)
2. The formula in #1 works because CHOOSE creates an array of the 3 non-adjacent cells and effectively makes them appear ‘adjacent’ to each other.
3. The Rank correlation is just the correlation of the ranks, and to get the Rank correlation, I just need to convert the values in cells U7, AM7, and BE7 to ranks. (The values in HR1:HT1 are already ranks.)
4. If the non-adjacent values in U7, AM7, and BE7 were adjacent to each other (e.g., in cells U7:U9), I could convert the values to their respective ranks and get the Rank correlation like this:
=CORREL(RANK.AVG(U7:U9,U7:U9),HR1:HT1)
5. Consequently, I thought I could simply substitute the adjacent values created by “CHOOSE({1;2;3},U7,AM7,BE7)” in place of the naturally occurring adjacent values in (U7:U9) in the formula in #4 to get the Rank correlation, something like this:
=CORREL(RANK.AVG(CHOOSE({1;2;3},U7,AM7,BE7),CHOOSE({1;2;3},U7,AM7,BE7)),HR1:HT1)
Unfortunately, this doesn’t work, either as a regular formula or an array formula. Nor do these ‘unions’ work:
=CORREL(CHOOSE({1;2;3},RANK((U7,AM7,BE7),(U7,AM7,BE7))),HR1:HT1)
=CORREL(RANK.AVG((U7,AM7,BE7),(U7,AM7,BE7)),HR1:HT1)
I could get the answer by adding 10 more columns to my spreadsheet, but I don't want to do that. I need to get the Rank Correlation in one formula.
Can anyone figure out how to write such a formula?
Thanks for your help.
1. In a single formula, I am trying to get the Rank (Spearman) correlation between two arrays. One of the arrays contains non-adjacent values. I can get the Pearson correlation with this formula:
=CORREL(CHOOSE({1;2;3},U7,AM7,BE7),HR1:HT1)
2. The formula in #1 works because CHOOSE creates an array of the 3 non-adjacent cells and effectively makes them appear ‘adjacent’ to each other.
3. The Rank correlation is just the correlation of the ranks, and to get the Rank correlation, I just need to convert the values in cells U7, AM7, and BE7 to ranks. (The values in HR1:HT1 are already ranks.)
4. If the non-adjacent values in U7, AM7, and BE7 were adjacent to each other (e.g., in cells U7:U9), I could convert the values to their respective ranks and get the Rank correlation like this:
=CORREL(RANK.AVG(U7:U9,U7:U9),HR1:HT1)
5. Consequently, I thought I could simply substitute the adjacent values created by “CHOOSE({1;2;3},U7,AM7,BE7)” in place of the naturally occurring adjacent values in (U7:U9) in the formula in #4 to get the Rank correlation, something like this:
=CORREL(RANK.AVG(CHOOSE({1;2;3},U7,AM7,BE7),CHOOSE({1;2;3},U7,AM7,BE7)),HR1:HT1)
Unfortunately, this doesn’t work, either as a regular formula or an array formula. Nor do these ‘unions’ work:
=CORREL(CHOOSE({1;2;3},RANK((U7,AM7,BE7),(U7,AM7,BE7))),HR1:HT1)
=CORREL(RANK.AVG((U7,AM7,BE7),(U7,AM7,BE7)),HR1:HT1)
I could get the answer by adding 10 more columns to my spreadsheet, but I don't want to do that. I need to get the Rank Correlation in one formula.
Can anyone figure out how to write such a formula?
Thanks for your help.